#1 2019-02-04 02:02:24 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
中央之帝爲混沌

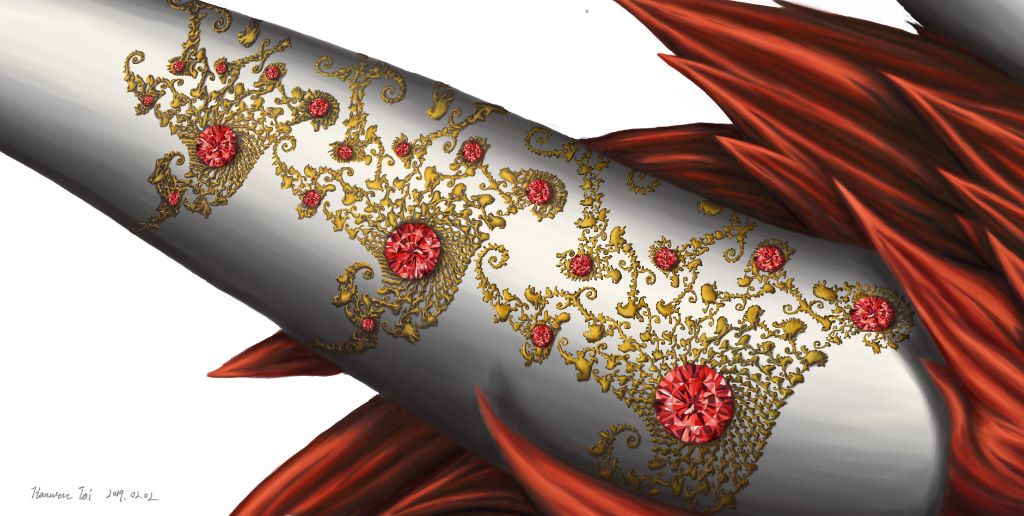
這算是我第一次畫的真正意義上的龍,是送給一個朋友的禮物,因爲朋友喜歡Digimon的Examon,所以特徵來自於他,鱗片排布參考了正在想的一個Avantar(其實也是找很多很棒的作者的作品參考的)。希望大家也能夠喜歡^ ^。
Landau最後未完成主持的朗道勢壘應試者,復旦大學教授郝柏林院士(老先生去年3月7日已經走了,按其遺願沒有設任何追悼會,旦大今年三月會在這個日子開一個理論物理研討會來紀念先生)1984年在新加坡世界科學出版公司出版了《混沌》,其扉頁上便引用了《莊子》裏的一段話:“The Emperor of the Central Region was called Hun-tun(Chaos)(中央之帝爲混沌).”
出處的全文是:“南海之帝爲倏,北海之帝爲忽,中央之帝爲混沌。倏與忽時相與遇於混沌之地,混沌待之甚善。倏與忽謀報混沌之德,曰:"人皆有七竅,以視聽食息,此獨無有,嘗試鑿之。"日鑿一竅,七日而混沌死。“
倏喻有象也,忽喻無形也。以前看這段話感覺也許是和其他創世神話類似的,比如說埃及的宇宙觀裏,被稱爲Nun的洪水過後,留下了混沌廢墟,太陽神Ra誕生其中。混沌是世界之前的樣子,和聖經一樣,經過了七天,纔有了一切,奇怪的是當時看還感覺這是個有點傷感的故事,可能是有點擬人化的原因吧…現在來看感覺頗有一種之前我們把世界放進了框框條條之中,反而使我們的更不能認識世界的感覺。
近代力學的偉大成就使得我們以機械觀來看待宇宙,像是一臺精密的鐘表,表面混雜的事物與過程,其背後一定有確定的規則。但在二十世紀末,自組織理論與非線性科學徹底改變了一切,彷彿回到了希臘Hesiod的時代,一個構成論與生成論互相廝殺的年代。Poincare在三體問題中第一次看到混沌時,他所認識的混沌是一種整體性。一般我們在處理一些非線性問題時,會用一些攝動法來把它線性化,比如Seidel微擾程函。但這些辦法同時也指出某些臨界情況下微小的異常卻帶來翻天覆地的變化。混沌看似與整體對立,但其實整體性是混沌的核心。通常,微小的變化最終只對結果產生很小的修正。但在臨界條件下,軌道與引力的種種變化互爲反饋累計到最後共振,整體效應擴大爲混沌。
現在來看,這個世界的根本是混沌的,線性的可解析的寥寥無幾甚至只是理想,
要去探求的是一種混沌序。在哲學與社會科學領域也伴生了反對還原主義的後現代性思潮,小的社會組織乃至是個體在整個社會中所起到的重要作用。整個人類社會現在像是站在了一個混沌分岔點上。
《周易》第一卦,乾卦:“元,亨,利,貞。初九:潛龍,勿用。九二:見龍在田,利見大人。九三:君子終日乾乾,夕惕若。厲無咎。九四:或躍在淵,無咎。九五:飛龍在天,利見大人。上九:亢龍,有悔。用九:見羣龍無首,吉。”,實際上在其標準譯本中,“乾”被譯爲“CH’IEN-THE CREATIVE”,有些外國學者比如J. Briggs認爲這段體現了一種混沌開放性與自組織創造性的聯繫。將龍視爲滿載電荷的雲層背後蘊含着的無窮威力,瞬息萬變,驚天動地。註釋中也有“其能量不受宇宙中任何固定條件的限制,他就是運動變化的本身。”
記得春秋時期的龍貌似是獸身有翼的,和經典的dragon形象非常像…一直感覺不同文明早期神話都很趨同這一點很有意思。
的確,龍在我心中有一種很微妙的地位...
另外之前想設計一套分形的飾品,就想一起做了。
飾品是基於分形的,所謂“分形是空間的混沌,混沌是時間的分形”
第一個要介紹的是左角的洛倫茲吸引子(Lorentz Attractor)


這個可能第一次看起來會感覺和其他的三個風格有點不一樣,我選他主要是因爲這個有比較重要的意義,他是第一個被發現的混沌吸引子,拉開了混沌學的序幕,洛倫茲吸引子又被稱爲蝴蝶吸引子。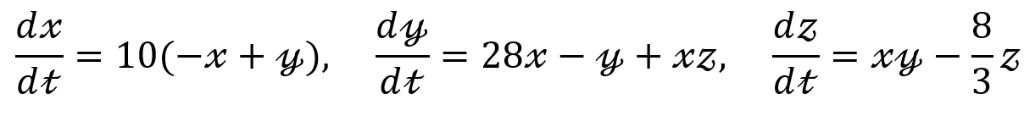
這套一階常微分方程組描述了一個二維的流體層均勻地從下面加熱,從上面加熱的系統。其中的x是對流比率,y是水平溫度梯度,z是豎直溫度梯度。10是Prandtl數,表明溫度邊界層和流動邊界層的關係,反映流體物理性質對對流傳熱過程的影響,28是Rayleigh數,超臨界的情況下反映傳熱形式主要爲對流,最後的8/3是流體層的物理維度,這裏可能看到一個分數的維度會感覺很奇怪,但爲描述分形結構需要分數維,這是一個與傳統幾何很不一樣的地方。
這個一階常微分方程組咋一看感覺很單純美好,但它的耦合的非線性項使得它沒辦法被解析解出。那所謂“天滅解析,數值大法好”,於是洛倫茲用起了計算機做數值解,他爲了運算效率把6位小數的數據,保留成3位小數來進行運算,如果這是一個線性系統的話,差一個三位的小數反映到結果上也只是一個千分之一微擾。但結果可以說是完全不一樣……他洞見到了這種對初始條件的敏感依賴性,所謂的“蝴蝶效應”。
把這個方程組畫到相空間裏面就是上面那個圖的樣子。我取的是差不多XOZ看過去的相軌跡的圖形。

上面那個連接結構是Newton集,形成原理和上面的有點不一樣,它是利用迭代規則和初始值反覆迭代,把點畫到複平面上得到的圖形。
init:
c = #pixel
#z = sqrt((1 - c)/6)
loop:
z2 = z * z
z3 = z * z2
z4 = z * z3
Err = (z4 + (c - 1)*z2 - c) / (4 * z3 + 2*(c - 1) * z)
z = z - Err
接下來是四個墜子的連接結構,都是Julia集,也是迭代生成,其迭代規則爲:
f(z)=z^2+c
C是公式裏的常數,被稱爲Julia種子,依靠簡單的公式與一個複數迭代產生了如此豐富的圖像,頗有一種“一生三,三生萬物”的感覺,也如英國詩人William Black的詩句
“To see a World in a Grain of Sand
And a Heaven in a Wild Flower,
Hold Infinity in the palm of your hand
And Eternity in an hour.”
我這裏一般會在吸引子處放一顆紅寶石。
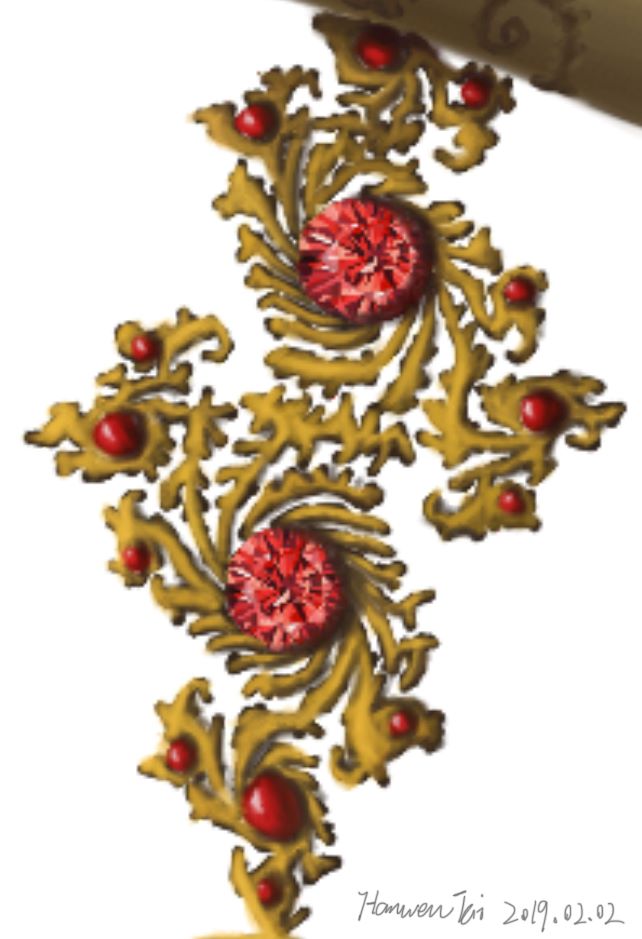
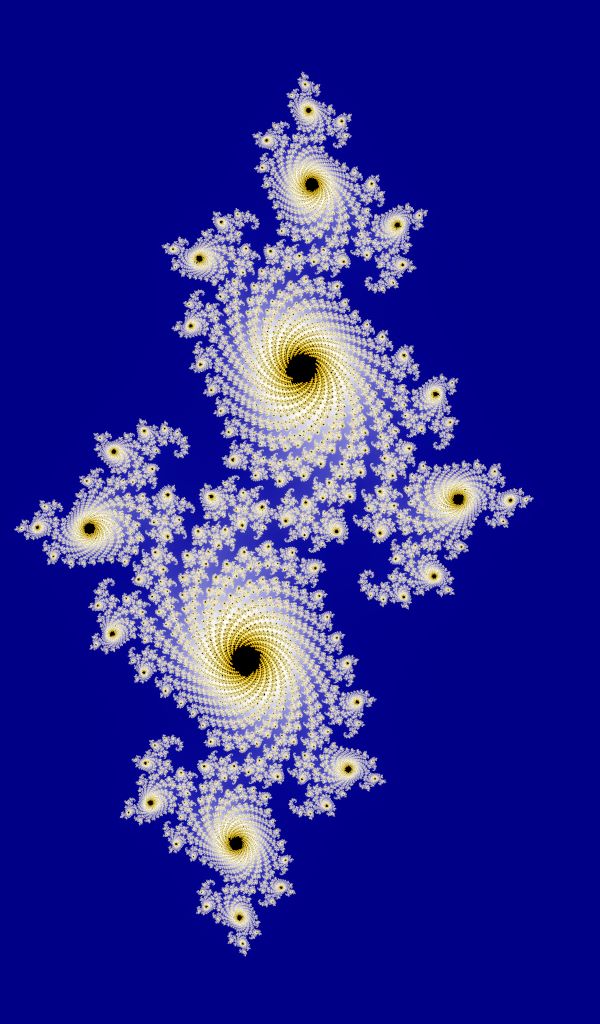
c = −0.7269 + 0.1889i


c = −0.8 + 0.156i


c=-0.74543+0.11301i


這一個當時沒有保留參數,記不得是多少了,抱歉…
接下來是最重要的Mandelbrot集,很多東西都是從這裏面來的,Mandelbrot是分形幾何的創始人,也是相當有趣的一個人。
它的迭代規則也是
f(z)=z^2+c
Mandelbrot集是從0開始的,它一直放大充斥着自相似的結構:






這裏用了一個Mandelbrot相似的子集來代替做了墜子的原型,因爲這個細節多一點。


角根套是用這個捲起來做的

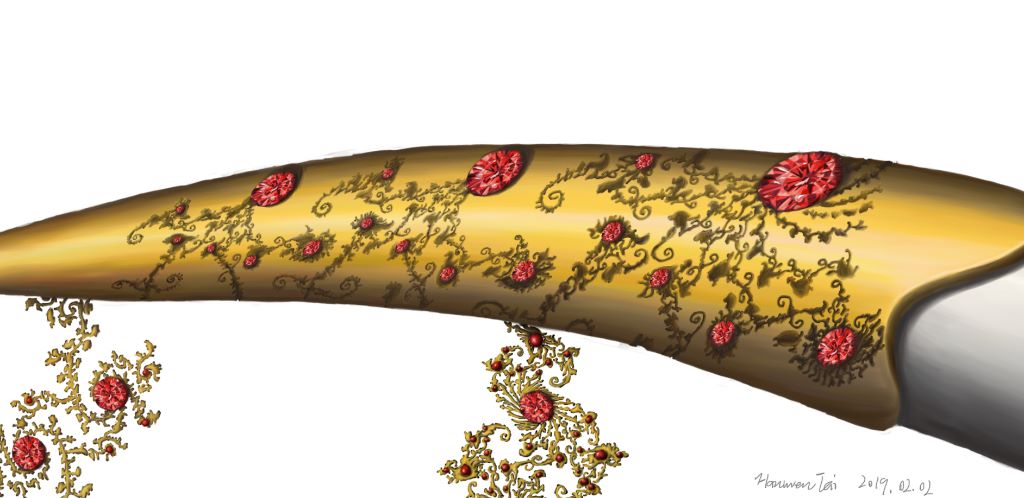
尖套也是,簡化版的內刻,不過效果不是特別好xwx
有一個小角戒也用了這個的子集


第二個小角戒

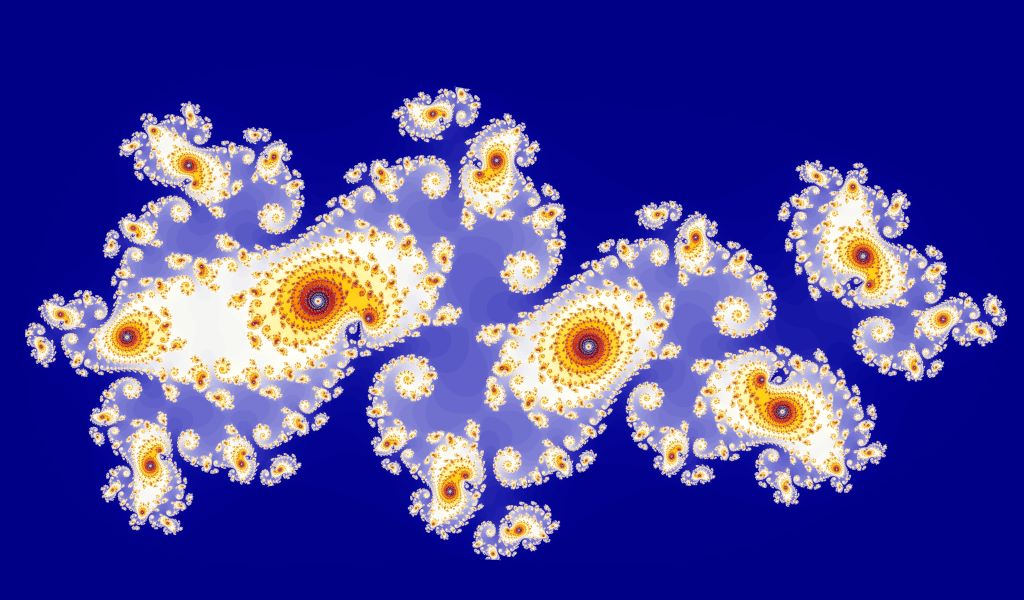
這個的迭代規則爲
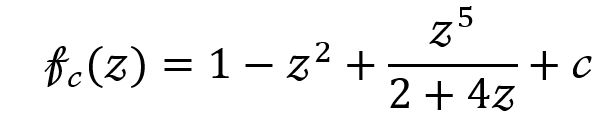
第三個小角戒
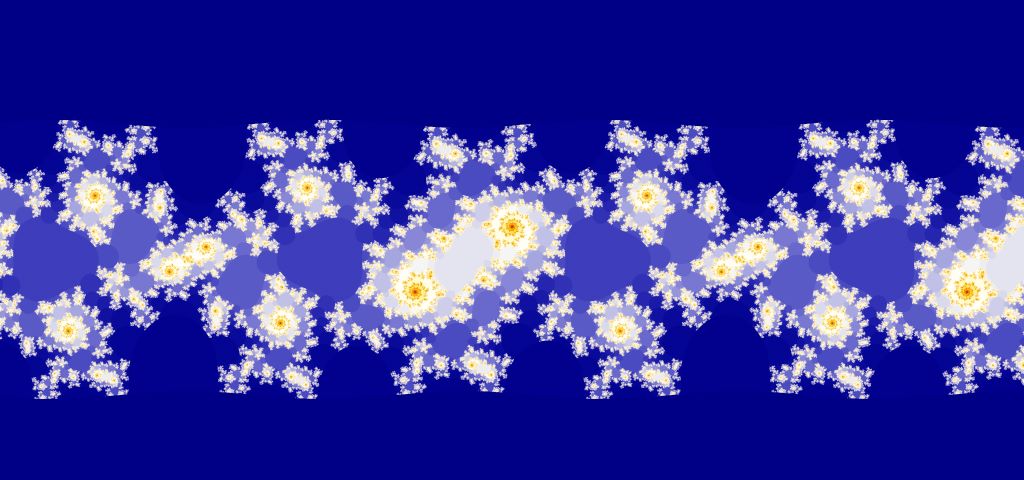
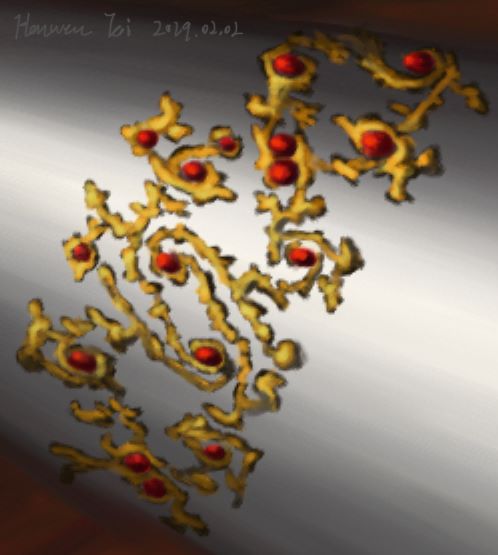
這個形成有點複雜,不是單純公式生成的,就不貼了
撞角套是兩個組成的



init:
z=pixel^2
loop:
z = z^@power+@seed
if(@Morph==true)
z=z-imag(z)
else
z=z
endif
if(@invert==true)
z=1/z
else
z=z
maxiter=1000
param seed
caption="Julia seed"
default=(0.3141,-0.5)
第三個墜子,太陽


這個是基於Julia集換迭代模式搞出來的,比較複雜涉及到軟件內置的迭代模式,就不粘代碼了
第四個墜子,月亮


這個是分形的另一種產生模式,幾何的自相似累積,相似的還有經典的三角形和四邊形做的

這兩個多少有點司辰司夜的感覺...
以下是細節展示,因爲這是送給朋友的畫,沒法給大家原圖,但這幅畫細節很多,可能縮略版本看不出來,很抱歉...

脖側脊鱗

頂鱗

腹面脖子

腹面鱗片

角根鱗

角根鱗細節

眉鱗與額鱗

面部小鱗

面頰鱗
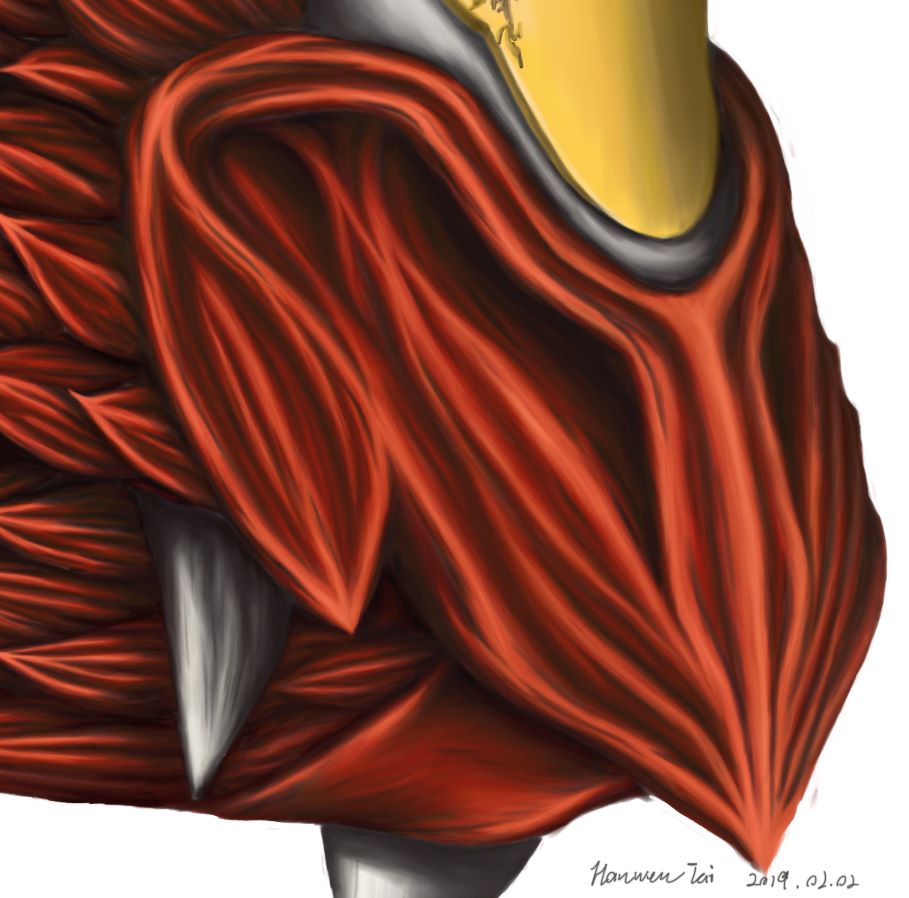
吻

眼
這裏的眼皮我參考了爬行動物的那種皮質感

眼後焰狀鱗
如果大家想要一個3M的jpg的話請到我的DA上找
https://www.deviantart.com/hanwentai
希望大家喜歡^ ^
有 12 位朋友喜欢这篇文章:shiningdracon, 龍爪翻書, MorksAllen, 地球遗龙, YellowBamboo, peter860321, Immortaldragon, efritshiva, 青鳞, 火柴龍, 安德Endur~, Drasiam

"Αὐτοῦ γὰρ καὶ Ῥόδος καὶ πήδημα"
离线
#2 2019-02-04 09:29:03 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
回应: 中央之帝爲混沌
@σπήλαιο_φυλακισμένο 寫道: 二維的流體層均勻地從下面加熱,從上面加熱的系統。
從上面冷卻,這裏有點筆誤,抱歉...

"Αὐτοῦ γὰρ καὶ Ῥόδος καὶ πήδημα"
离线
#3 2019-02-04 11:16:12 | 只看该作者
- 龍爪翻書
- 会员

- 来自 台北
- Registered: 2011-07-10
- Posts: 2,954
回应: 中央之帝爲混沌
用分形來做珠寶設計,我是第一次見到呢
←目前頭像感謝安雅贈圖。

Quit, dont quit... Noodles, dont noodles...
There is a saying: yesterday is history, tomorrow is a mystery, but today is a gift. That is why it is called the present.
离线
#4 2019-02-04 12:24:58 | 只看该作者
- Nemiriz
- 蛟龍

- Registered: 2018-11-24
- Posts: 393
回应: 中央之帝爲混沌
太厲害了
什麼時候我才能會畫鱗片和珠寶啊啊啊啊dawjdkaad
离线
#5 2019-02-04 16:37:40 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
回应: 中央之帝爲混沌
可能是因爲它是分數維的,理論上邊長是無限的...即使實際上是有簡化的,但實際上在一個狹小空間內仍有很精密的結構,所以加工是非常困難的...我之前也沒有見過有類似的作品,但我敢肯定有這個想法的人應該不在少數,因爲分形的審美價值的確非常高
@Nemiriz 寫道: 太厲害了什麼時候我才能會畫鱗片和珠寶啊啊啊啊dawjdkaad
沒有什麼啦...其實這幅畫是我第一次畫真正義意上的龍,所以畫鱗片和飾品也是第一次。有了好的點子去耐心多試試,一般是會有比較符合期望的產出的。
有 1 位朋友喜欢这篇文章:龍爪翻書

"Αὐτοῦ γὰρ καὶ Ῥόδος καὶ πήδημα"
离线
#6 2019-02-05 17:57:51 | 只看该作者
- shiningdracon
- 寻道龙

- Registered: 2008-11-03
- Posts: 4,346
回应: 中央之帝爲混沌
好漂亮。
同是第一次見到用分形來做珠寶設計,也是第一次見到分形被用在龍圖創作上。
自己也有想過能不能用函數擬合出龍的輪廓,哪怕抽象一點。
以龍為本
<-- 目前頭像 by 理業化肥
聯繫方式:站內短消息或郵件
离线
#7 2019-02-05 19:11:39 | 只看该作者
- 龍爪翻書
- 会员

- 来自 台北
- Registered: 2011-07-10
- Posts: 2,954
回应: 中央之帝爲混沌
@σπήλαιο_φυλακισμένο 寫道: 可能是因爲它是分數維的,理論上邊長是無限的...即使實際上是有簡化的,但實際上在一個狹小空間內仍有很精密的結構,所以加工是非常困難的...我之前也沒有見過有類似的作品,但我敢肯定有這個想法的人應該不在少數,因爲分形的審美價值的確非常高
金屬的部份,只要有模型,都可以翻模鑄造的 ![[靈感]](/forum/img/smilies/haku/haku-idea.svg)
模型的部份可以用3D列印來做
1. 3D模型檔案
2. 3D列印
3. 翻模、鑄造
4. 拋光、電鍍
5. 鑲寶石
←目前頭像感謝安雅贈圖。

Quit, dont quit... Noodles, dont noodles...
There is a saying: yesterday is history, tomorrow is a mystery, but today is a gift. That is why it is called the present.
离线
#8 2019-02-06 16:35:17 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
离线
#9 2019-02-06 22:34:54 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
回应: 中央之帝爲混沌
[↑] @shiningdracon 寫道: 好漂亮。 同是第一次見到用分形來做珠寶設計,也是第一次見到分形被用在龍圖創作上。 自己也有想過能不能用函數擬合出龍的輪廓,哪怕抽象一點。 …
謝謝您的鼓勵^ ^
函數擬合的話實際有很多軟件方便做的,Wolfram 公司的官方博客以前就做過一些名人的頭像擬合,
https://blog.wolfram.com/2013/05/17/making-formulas-for-everything-from-pi-to-the-pink-panther-to-sir-isaac-newton/
http://blog.wolframalpha.com/2013/06/10/using-formulas-for-everything-from-a-complex-analysis-class-to-political-cartoons-to-music-album-covers/
https://blog.wolfram.com/2013/08/15/even-more-formulas-for-everything-from-filled-algebraic-curves-to-the-twitter-bird-the-american-flag-chocolate-easter-bunnies-and-the-superman-solid/
這些比較複雜,但實際上一些比較簡單的平滑處理和Mathematica的讀邊函數和傅里葉級數擬合就可以得到。
這裏我用Wales的Red Dragon爲例子來做一個函數畫龍

這裏先把最大項數調到100,採用的參數形式,所以會得到200個項來描述一個曲線
由於識別上的原因會有些雜曲線,只提取藍色曲線的函數作圖,藍色框出的就是x的參數方程
最後得到: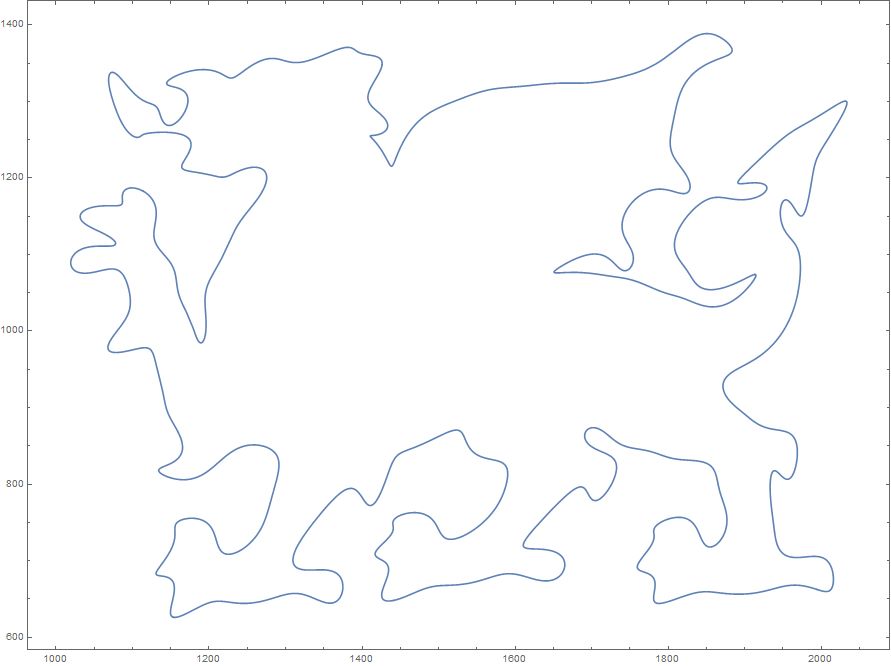
改變最大項數得到的其他結果:
10項:
50項:
500項: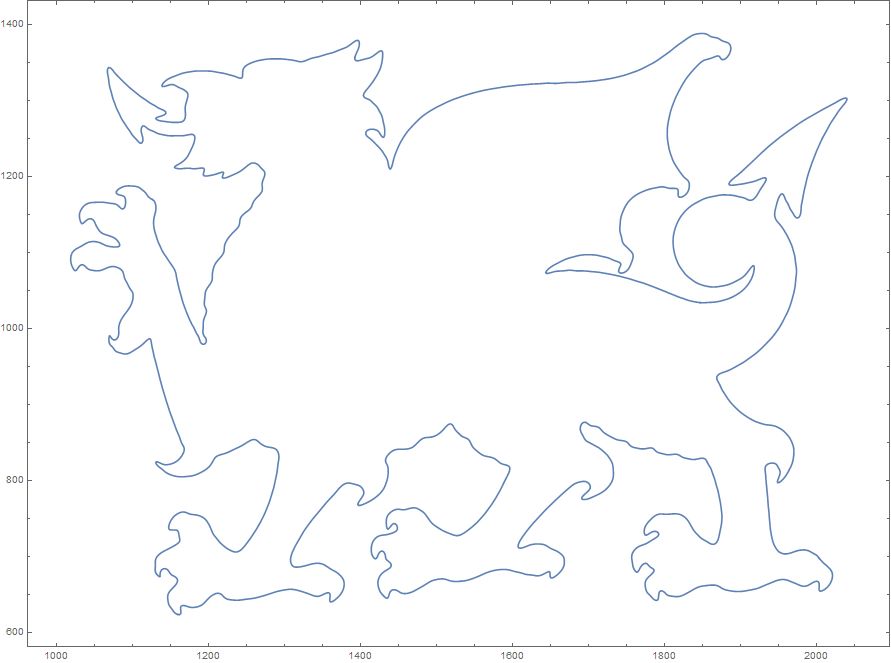
到50項纔有還算能看出來的效果,私以爲這種有過多參數的沒什麼美感...就像物理裏那種特別長的解析解一樣,沒太大意義...
就像當時Fermi引用von Neumann的話吐槽Dyson:”With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.“
也就是所謂的”四個參數畫大象,五個讓他鼻子搖“
後來有篇論文還真在討論這個問題
https://publications.mpi-cbg.de/getDocument.html?id=ff8080812daff75c012dc1b7bc10000c
他用很簡單的複變函數表示出了大象,也真的讓他鼻子搖起來了
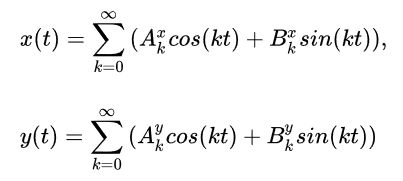
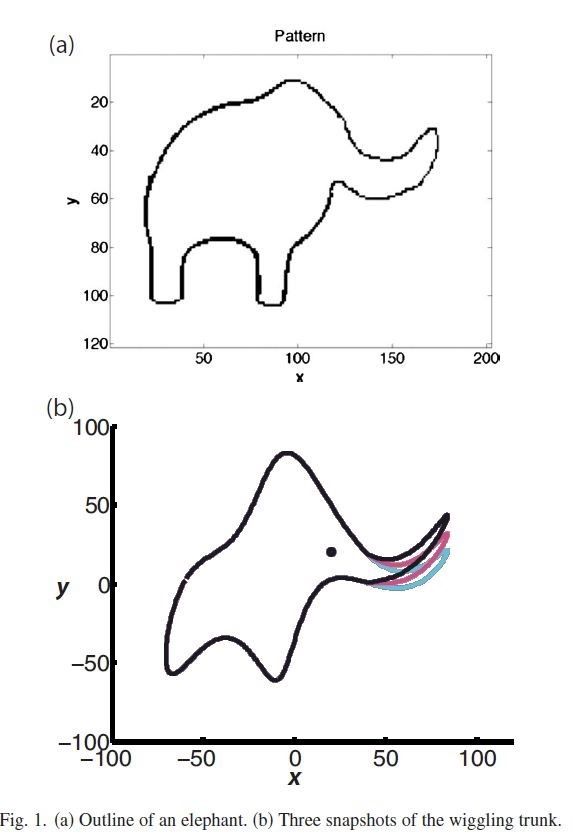
不過如果把原圖像設計簡單一些並且神韻很好的話,應該是可以用比較少的項得到比較好的結果的,關於後面那種論文裏那種,這個可以用已知方程去做擬合。
就可以來“With four parameters I can fit a dragon, and with five I can make him flap his wings.“
有 2 位朋友喜欢这篇文章:shiningdracon, 龍爪翻書

"Αὐτοῦ γὰρ καὶ Ῥόδος καὶ πήδημα"
离线
#10 2019-02-14 18:28:48 | 只看该作者
- Honestraz
- 虬龍

- 来自 龍眠界域
- Registered: 2014-06-02
- Posts: 158
回应: 中央之帝爲混沌
好厲害!! ![[被雷]](/forum/img/smilies/haku/haku-shock.svg)
沒想到寫程序還能跟畫畫結合在一起!
還有沒有類似的作品呀
隨心所欲,隨風而去,
雙翼欲展,與心同在。
願我之心,與龍同在,
日落之時,翔於雲彩。
离线
#11 2019-02-15 14:58:18 | 只看该作者
- σπήλαιο_φυλακισμένο
- 虺龍

- 来自 南京
- Registered: 2018-12-30
- Posts: 30
回应: 中央之帝爲混沌
[↑] @Honestraz 寫道: 好厲害!!
沒想到寫程序還能跟畫畫結合在一起! 還有沒有類似的作品呀
…
謝謝您支持^ ^,如果您有興趣的話可以去我的DA看看,那裏有我的一些東西,還有些可能以後會用到其他地方,暫時沒有上傳到網上。
https://www.deviantart.com/hanwentai/gallery/

"Αὐτοῦ γὰρ καὶ Ῥόδος καὶ πήδημα"
离线
 爪機版
爪機版 天鳞鳞,地鳞鳞
天鳞鳞,地鳞鳞![[微笑]](/forum/img/smilies/haku/haku-smile.svg)
![[流鼻血]](/forum/img/smilies/haku/haku-nosebleeds.svg)